معلومات عامة (1)
الدائرة في المرحلة الثانوية تختلف جذرياً عنها في المرحلة الإعدادية فهنا ندرس الصور المختلف لمعادلة الدائرة وعلاقتها بدائرة أخرى أو مستقيم من حيث الوضع وأمور أخرى تركز في غالبيتها على المعادلات، ولكن سنستعين بالعديد من الأفكار التي دُرست في المرحلة الإعدادية ليس في الدائرة فقط بل في الهندسة بصورة عامة.
سنقسم موضعنا هذا إن جاز لنا التعبير (المسابقة) لعدة أقسام
1) معادلة الدائرة بصورها المختلفة
2) علاقة دائرة بدائرة أخرى أو مستقيم
3) التماس
4) المحل الهندسي
=======================================
معادلة الدائرة التي مركزها ( د ، هـ) ونصف قطرها نق هي: 

( س – د)2 + ( ص – هـ)2 = نق2 نق نصف قطر الدائرة
نحصل على هذه المعادلة من استخدام قانون البعد بين نقطتين
مربع البعد بين النقطتين ( س1 ، ص1) ، ( س2 ، ص2) هو:
مربع البعد بين النقطتين = ( س2 – س1)2 + ( ص2 – ص1)2
وبتطبيقه على البعد نق الواصل بين ( س ، ص) ، ( د ، هـ)
مع ملاحظة ( د ، هـ) أي نقطة في مستوى الإحداثيات الديكارتيه والشكل المرفق توضيح لذلك.

معادلة الدائرة التي مركزها نقطة الأصل ونصف قطرها نق
وفي حال كون د = 0 ، هـ = 0 أي ( د ، هـ) تكون نقطة الأصل
فإن معادلة الدائرة تؤول إلى س2 + ص2= نق2
وهي معادلة الدائرة التي مركزها نقطة الأصل ونصف قطرها نق
ويمكن الحصول عليها مباشرة من الشكل باستخدام نفس القانون
السابق وهو البعد بين نقطتين.
معادلة الدائرة التي طرفا قطر فيها ( س1 ، ص1) ، ( س2 ، ص2) هي:
( س – س1) ( س – س2) + (ص – ص1)( ص – ص2) = 0

يمكن الحصول عليها من:
ق< د = 90ه < د مرسومة في نصف دائرة لاحظ الشكل
ميل ب د × ميل د هـ = – 1 تعامد مستقيمين
الميل لمستقيم مار بنقطتين = فرق الصادات ÷ فرق السينات
ص – ص1 ص – ص2
ـــــــــــــــــــ × ـــــــــــــــــــــ = – 1
س – س1 س – س2
( س – س1) ( س – س2) = –(ص – ص1)( ص – ص2)
( س – س1) ( س – س2) + (ص – ص1)( ص – ص2) = 0
الصورة العامة لمعادلة الدائرة:
من: ( س – د)2 + ( ص – هـ)2 = نق2 وبفك الأقواس نحصل على
س2 + ص2–2 د س –2هـ ص + د2+ هـ2– نق2 = 0 وبوضع د= – ل ، هـ = – ك ، د2 + هـ2– نق2 = حـ يكون:
س2 + ص2 + 2 ل س + 2 ك ص + حـ = 0 مركزها (– ل ، – ك) ونصف قطرها نق حيث نق2= ل2 + ك2 – حـ
لاحــــــــظ:
1) لإيجاد المركز من المعادلة نجعل معامل س2= معامل ص2= 1 ثم المركز = (– معامل س÷2 ، – معامل ص÷2)
2) إذا مرَّ محيط الدائرة بنقطة الأصل فإن حـ = 0 والعكس صحيح لأن س = ص = 0 وتؤول المعادلة إلى:
س2 + ص2 + 2 ل س + 2 ك ص = 0
حالات خاصة:

1) إذا وقع المركز م = (– ل ، – ك) على محور السينات
فإن ك = 0 (إي نقطة تقع على محور الصادات إحداثها السيني =0)
أي م = (– ل، 0) وتصبح معادلة الدائرة:
س2 + ص2 + 2 ل س + حـ = 0
ويكون ل2 + ك2 – حـ = نق2 ( ك = 0 )
أي أن: ل2– حـ = نق2
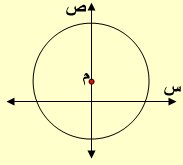
2) إذا وقع المركز م = (– ل ، – ك) على محور الصادات
فإن ل = 0 (إي نقطة تقع على محور الصادات إحداثها السيني =0)
أي م = (0 ، – ك) وتؤول معادلة الدائرة:
س2 + ص2 + 2 ك ص + حـ = 0
ويكون ل2 + ك2 – حـ = نق2 ( ل = 0 )
أي أن: ك2– حـ = نق2

3) إذا مسَ محيط الدائرة محور السينات
فإن ك = نق
أي ك2= نق2
ومن: ل2+ ك2– حـ = نق2
ل2– حـ =0
ل2 = حـ

3) إذا مسَ محيط الدائرة محور الصادات
فإن ل = نق
أي ل2= نق2
ومن: ل2+ ك2– حـ = نق2
ك2– حـ =0
ك2 = حـ
3) إذا مسَ محيط الدائرة محور السينات فإن ك = ل = نق 

والمركز هنا ( نق ، نق ) وتوجد 4 دوائر حسب موقـــع
المركز في أي ربع من الأرباع الأربعة.
( س – نق)2 + ( ص – نق)2 = نق2
( س + نق)2 + ( ص – نق)2 = نق2
( س + نق)2 + ( ص + نق)2 = نق2
( س – نق)2 + ( ص + نق)2 = نق2


